Kellerautomaten und Turingmaschinen
Eine äußerst interessante Frage ist, ob ein solcher Automat alle typischen Aufgaben aus der Programmierung übernehmen kann. Um ein kompliziertes Beispiel zu nennen, könnte ein solcher Automat die syntaktische Richtigkeit eines JAVA-Programms überprüfen. Ein Computer kann das, wie man noch aus dem JAVA-Kurs weiß.
Dazu vereinfachen wir das Problem: kann ein Automat einen mathematischen Term auf Korrektheit überprüfen. Dazu müsste die Sprache des Automaten genau alle korrekten mathematischen Terme sein.
In diesem Zusammenhang muss natürlich auch geprüft werden, ob die Klammern alle korrekt gesetzt sind. Dazu müssen genauso viele Klammern geöffnet, wie geschlossen werden. (Natürlich gilt noch mehr: es dürfen von links gezählt nie mehr schließende als öffnende Klammern da sein). Aber selbst wenn wir annehmen, dass erst alle öffnenden Klammern kommen und erst danach alle schließenden, ist ein endlicher Automat damit überfordert.
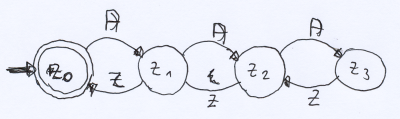
Wir könnten den Zustand Z1 für eine Klammer auf, Z2 für zwei Klammern auf, usw. verwenden. Beim Schließen würden wir einfach wieder rückwärts durch die Zustände wandern. Das Bild zeigt einen solchen Automaten für maximal drei Klammern am Anfang. Er kann auch öffnende und schließende Klammern gemischt verarbeiten, dann geht eventuell auch mehr als drei. (Eingabe A steht für Klammer auf, Z steht für Klammer zu)
Das Problem ist allgemein, dass ein korrekter mathematischer Ausdruck beliebig viele Klammern enthalten kann. So würde ein Ausdruck, bei dem 4 Klammern geöffnet werden, von unserem Automat nicht erkannt. Natürlich könnte man einen größeren für 4 oder 10 Klammern konstruieren. Die würden dann aber an 5, bzw. 11 Klammern scheitern. Zur Erinnerung: der endliche Automat hat nur endlich viele Zustände. Um ein solches Problem zu lösen, braucht der Automat zusätzlich einen im Prinzip unbegrenzten Speicher. Diese Forderung erfüllt ein Kellerautomat.
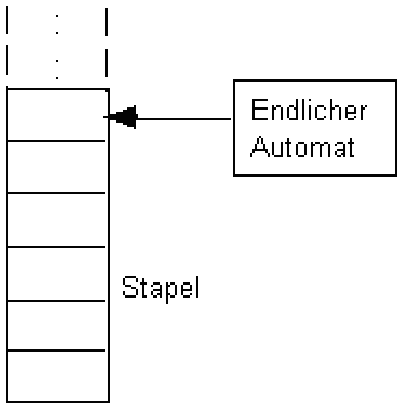
Bei jedem Übergang im endlichen Automaten wird festgelegt, ob etwas auf den Stapel gelegt wird (PUSH) oder etwas weggenommen wird (POP)oder nichts am Keller verändert wird (NOP). Es gibt ein Zeichen, das markiert, wenn der Stapel leer ist (bei uns #). Der Automat liest ein Zeichen ein, liest das oberste Zeichen auf dem Stapel und abhängig davon erfolgt der Übergang und damit die Operation am Stapel.
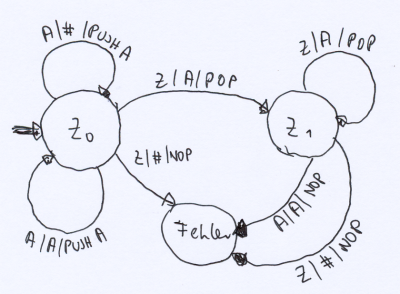
Das untere Bild zeigt den Kellerautomat, der in der Lage ist, gleich¬viele geöffnete Klammern und darauf folgende schließende Klammern zu erkennen, d.h. einen Ausdruck der Form AnZn
Dabei bedeutet an den Übe¬rgängen „eingegebenes Zeichen/oberstes Zeichen auf dem Stapel/Operation auf dem Stapel“.
Ein Ausdruck wird akzeptiert, wenn am Ende der Eingabe der Automat im Zustand Z1 ist und der Stapel leer (#).
Ansonsten wollen wir den Kellerautomaten nicht weiter verfolgen, sondern nur die Frage beantworten, ob ein Kellerautomat jetzt „alle Probleme“ lösen kann.
Dazu betrachten wir die Sprache AnBnCn, d.h. es werden alle Ausdrücke akzeptiert, die nacheinander gleich viele A’s, B’s und C’s enthalten. Wie man sich leicht überlegt, kann ein Kellerautomat solche Ausdrücke nicht nachprüfen. Er bräuchte dazu zwei Stapel.
Um jetzt nicht eine ganze Familie von Automaten mit zwei, drei usw. Stapel zu betrachten, hat man sich eine etwas universellere Maschine überlegt, die sogenannte Turing¬maschine, benannt nach dem Mathematiker Alan Turing (1912 – 1954), der unter anderem beim Bletchley Park-Projekt der Engländer an der Entschlüsselung der deutschen Chiffrier-maschine ENIGMA mitarbeitete.
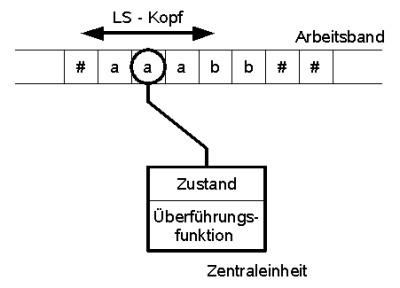
Eine solche Maschine besteht aus einem Speicherband, auf dem sich ein Schreib-Lesekopf nach links oder rechts jeweils um einen Schritt bewegen kann und einem endlichen Automaten. Ein Übergang zwischen zwei Zuständen wird gekennzeichnet durch das Lesen eines Eingabezeichens vom Band, dem Schreiben eines neuen Zeichens auf das Band an dieser Stelle und einer anschließenden Kopfbewegung nach links oder nach rechts (oder stehenbleiben).
Man kann zeigen, dass eine solche Turingmaschine den heutigen Computern im Prinzip äquivalent ist, d.h. ein Computer kann nicht mehr als eine Turingmaschine.
Auch mit Turingmaschinen wollen wir uns nicht weiter beschäftigen, zumal es eine äquivalente Form gibt, die sogenannte Registermaschine, die wesentlich leichter zu verstehen ist und viel mehr modernen Prozessoren ähnelt.
Eine Turingmaschine lässt sich auch durch eine Tafel beschreiben, eine endliche Reihe von 5-Tupeln :
Zustand – gelesenes Zeichen – zu schreibendes Zeichen – Kopfbewegung - Folgezustand
 }}
}}