Die theoretische Informatik ist ein Teilgebiet der Informatik, welche sich mit grundlegenden Fragestellungen der Informatik befasst. Unter anderem ist auch die Automatentheorie Inhalt dieses Teilgebiets.

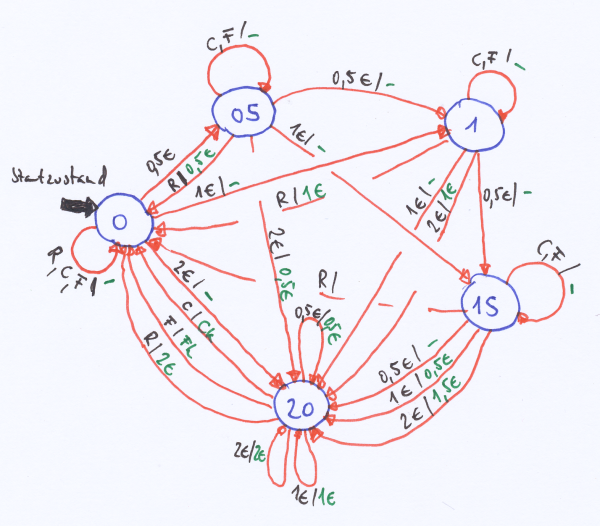
Wir betrachten einen Getränkeautomaten. Der Automat soll zwei verschiedene Getränke Cola und Fanta zum Preis von 2,00 € ausgeben. Der Automat akzeptiert 50-Cent-, 1-€- und 2€-Stücke. Der Automat soll einen Geldrückgabeknopf besitzen, damit man Geld zurück erhält zurück, wenn man es sich anders überlegt hat. Überzahltes Geld wirft der Automat automatisch aus. Dieser Automat lässt sich in einem Zustandsdiagramm sehr gut darstellen.

Die Kreise stehen dabei für die Zustände, die hier 0, 05, 1, 15 und 2 weisen. Dabei ist 0 der Startzustand des Automaten.

Die Pfeile beschreiben die Übergänge zwischen den einzelnen Zuständen in Abhängigkeit von der getätigten Eingabe (auf den Pfeilen vor dem Schrägstrich. Die möglichen Eingaben sind 0,5 €, 1 €, 2 €, C für Cola gewünscht , F für Fanta gewünscht und R für Geldrückgabe. Damit der Automat nicht in einen undefinierten Zustand gerät, muss er für alle 5 Zustände auf jede Eingabe reagieren können, d.h. es müssen von jedem Zustand 6 Pfeile ausgehen. Zu jedem Übergang gehört auch eine Ausgabe (hinter dem Schrägstrich). Unser Automat hat keine Endzustände. Diesen speziellen Automaten nennt man Mealy-Automat.

Fassen wir das noch mal allgemein zusammen

Ein endlicher Automat besteht aus

1. einer Menge von Eingaben, dem Eingabealphabet.
2. (event.) einer Menge von Ausgaben, dem Ausgabealphabet.
3. einer Menge von Zuständen
4. einem Startzustand aus der Menge der Zustände
5. (event.) ein oder mehreren Endzuständen aus der Menge der Zustände
6. einer Übergangsfunktion, die jeder Kombination Zustand-Eingabe einen Folgezustand zuordnet.
7. (event.) einer Ausgabefunktion, die jeder Kombination Zustand-Eingabe eine Ausgabe zuordnet.

Übergangsfunktion und Ausgabefunktion lassen sich statt im Zustandsdiagramm auch in Tabellenform darstellen.

Der Getränkeautomat hat als Eingaben „0,5€, 1€, 2€, Cola(C), Fanta(F), Rückgabe(R)“ und als Ausgaben „Cola kommt(Ck)“, „Fanta kommt(Fk)“, 0,5€ (zurück), 1€ (zurück), 1,5€ (zurück), 2€ (zurück), Nichts zurück (-)“.

1. Stellen Sie beim Colaautomat Übergangsfunktion und Ausgabefunktion in Tabellenform dar.
2. Ein Spielautomat (Einarmiger Bandit) hat nur die Gewinnstufe 3 €. Jedes Spiel startet durch Druck auf einen Knopf und kostet (egal ob Gewinn oder Verlust) 1 €. Der Automat akzeptiert 1 € und 2 € Stücke. Es kann jederzeit beliebig Geld eingeworfen werden, allerdings bis maximal 5 €. Überschreitet das Guthaben durch Einwurf oder Gewinn die 5 €, dann wird das überzählige Geld ausgeworfen. Es gibt einen Geldrückgabeknopf, der das komplette Guthaben auszahlt. Entwirf den oben beschriebenen Automat und erläutere gegebenenfalls deine Überlegungen. Gib konkret alle Bestandteile dieses endlichen Automaten an.
3. Ein altes Rätsel lautet: Ein Bauer, der einen Wolf, eine Ziege und einen Kohlkopf dabei hat, muss einen Fluss überqueren. Das Boot ist aber so klein, dass er nur eines der Dinge mitnehmen kann. Lässt er jedoch Wolf und Ziege auf einer Seite des Ufers allein, frisst der Wolf die Ziege. Genauso ergeht es dem Kohlkopf, wenn er mit der Ziege allein ist. Wie kann der Bauer alle Dinge unbeschadet ans andere Ufer bringen? Erstelle dazu einen endlichen Automaten mit geeigneten Zuständen. Zur Vereinfachung können alle Übergänge, die zum Verlust eines der Dinge führen und damit das Rätsel nicht lösen weggelassen werden. Welche Bestandteile muss der Automat haben, welche nicht?
4. Ein Automat verkauft Fahrkarten im Wert von 3€ und zwar nimmt er Ein- und Zwei-Eurostücke an. Sobald genügend Geld eingeworfen ist, fällt die Fahrkarte in das Entnahmefach, zu viel eingeworfenes Geld wird nicht zurückgegeben. Entwirf den beschriebenen Automat und erläutere gegebenenfalls deine Überlegungen. Gib konkret alle Bestandteile dieses endlichen Automaten an.
5. Der Automat Hund wird wie folgt charakterisiert: Eingabe: streicheln, knuffen Zustand: friedfertig, zweifelnd, wütend Ausgabe: wedeln, bellen Ist der Hund friedfertig, so folgt auf die Eingabe „streicheln“ die Ausgabe „wedeln“. Wird der friedfertige Hund geknufft, wedelt er weiter, geht aber in den Zustand zweifelnd. Wird der zweifelnde Hund gestreichelt, so wedelt er und wird friedfertig, wird er nochmals geknufft, so bellt er und wird wütend. Der wütende Hund reagiert auf knuffen mit bellen und bleibt wütend, auf streicheln bellt er weiter, wird aber friedfertig. Entwirf ein Zustandsdiagramm dieses Automaten.
6. Vier Kessel werden elektrisch beheizt, die Zuleitungen verkraften aber nur den gleichzeitigen Betrieb von zwei Kesseln. Entwickeln Sie einen endlichen Automaten und die zugehörige Schaltung, die die folgenden Signale erzeugt: W: Warten, keine weitere Heizstelle darf zugeschaltet werden. Z: Zuschalten, eine weiterer Kessel darf zugeschaltet werden. A: Alarm, mehr als zwei Kessel sind eingeschaltet.