Inhaltsverzeichnis
Deterministische Endliche Automaten
Auch der im vorherigen Kapitel angesprochene Mealy-Automat ist eine DFA. Für die Informatik von besonderer Bedeutung sind die sogenannten Akzeptoren oder erkennenden Automaten. Diese Typen sind auch viel häufiger anzutreffen als Mealy-Automaten. Akzeptoren sind endliche Automaten mit Anfangs und Endzuständen und ohne Ausgabe. Eine Folge von Eingaben, die vom Anfangszustand zu einem der Endzustände führt, heißt akzeptiertes Wort. Alle akzeptierten Worte bilden die Sprache des Automaten.
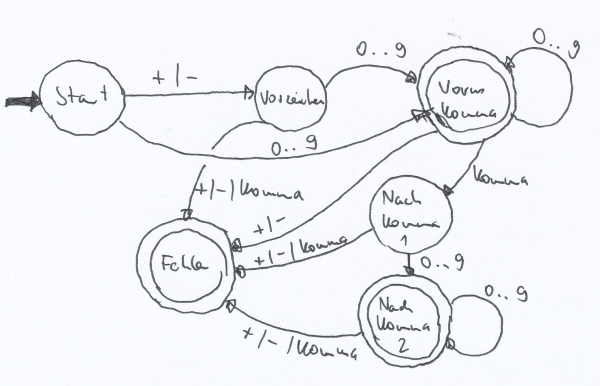
Die Sprache des Akzeptors soll eine normale Kommazahl sein. Das Eingabealphabet besteht aus {+,-,0,1,…,9,Komma}. Ausgaben gibt es ja nicht.
Aufgabe 1
Nennen Sie fünf auch von der Art verschiedene Zahlen, die zu der Sprache dieses Akzeptors gehören. Könnte man führende Nullen vermeiden?
- Ergänzen Sie den Automat so, dass er auch Zahlen in Exponentialschreibweise akzeptiert, z.B. 3,143E-02
- Entwickeln Sie einen Akzeptor, der vorzeichenlose Binärzahlen akzeptiert. Keine führenden Nullen!
- In der Theologie des Thomas von Aquin ist die Seele ein wunderbar ausgeklügelter Automat. Erschaffen im Stand der Schuld infolge der Erbsünde gelangt sie durch die Taufe in den Stand der Gnade. Gewisse Handlungen (Gotteslästerung, Ehebruch, Mord) bewirken einen Fall in den Stand der Schuld. Beichte, Reue und Absolution können den Stand der Gnade wieder herstellen. Die Wirkung des Todes hängt entscheidend vom Zustand der Seele im Augenblick des Todes ab: Im Stand der Gnade führt der Tod zur Erlösung, im Stand der Sünde zur Verdammnis.
- Zeichne den Zustandsgraphen des endlichen Automaten. Kennzeichne Eingabealphabet, Zustände, Startzustand, Übergangsfunktion, Ausgabealphabet, Ausgabefunktion, Endzustände.
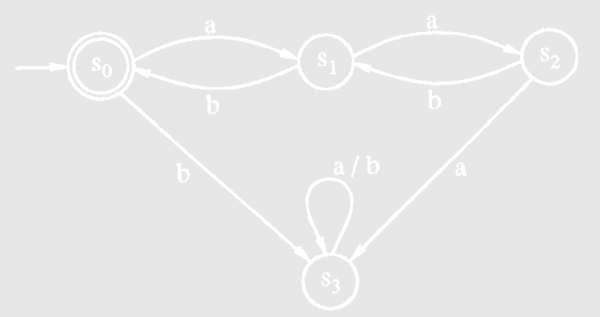
- Das folgende Bild zeigt einen Akzeptor.
Welche der folgenden Worte werden vom Automaten akzeptiert?
a (2) ab (3) aaabbb (4) ababab (5) baba
Finde drei Worte, die nicht oben vorkommen, die vom Automaten akzeptiert werden.
Beschreibe mit Worten die Sprache, die vom Automaten akzeptiert wird.
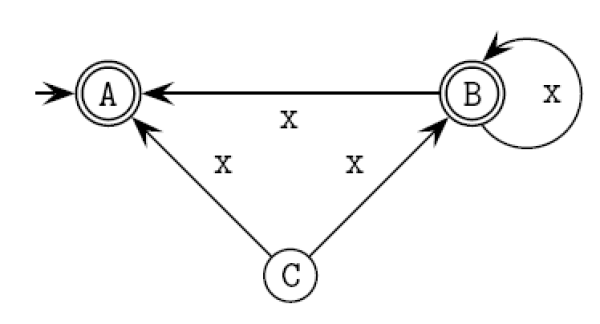
Aufgabe 3
Betrachte den folgenden endlichen Automat. Was ist an diesem Automaten „falsch“?
Welche Sprache akzeptiert der Automat?
 Erstelle einen endlichen Automaten über der Sprache {x,y}, der alle Wörter erkennt, die mit der Kombination „xy“ aufhören.
Erstelle einen endlichen Automaten über der Sprache {x,y}, der alle Wörter erkennt, die mit der Kombination „xy“ aufhören.
Aufgabe 4
Erstelle einen endlichen Automaten, der nur Binärzahlen akzeptiert, die eine gerade Zahl von Einsen und eine gerade Zahl von Nullen haben.
Aufgabe 5
Entwickle einen Automaten, der alle Wörter über dem Alphabet {a,b,c} erkennt, bei denen unmittelbar nach jedem a genau ein b kommt (Beispiele abc, bcab, babcb, aber nicht baab).